🚶 受動歩行機
足裏形状を最適化し、斜面傾斜角変化にロバストな受動歩行を実現する
目次
特徴
- 🦿 受動歩行:アクチュエーターや制御装置を使わない、重力を活用した歩行
- 🚶 形態学的知性: 身体のダイナミクスを活かし、生物のようにエネルギー効率のよい歩行を生成
- 🦶 最適化された足裏形状: 斜面の傾きが変わっても安定して歩行が継続できるように改良
概要
受動歩行機はエネルギー効率の高い歩行を実現しますが、斜面の傾きが変わると歩行が容易に不安定になるという課題があり、現実世界での実用化に障害があります。これまでの研究では、異なる傾斜角に合わせた足裏形状を使うことで安定性を向上させてきました。しかし、この方法では斜面ごとに異なる足裏形状を用意する必要があります。そこで、私たちは単一の最適化された足裏形状を使い、幅広い傾斜角に対応できる受動歩行機のデザイン手法を提案します。
受動歩行とは?
受動歩行機は、重力と自身のダイナミクスを利用して斜面を下りながら歩く仕組みです。この方法はエネルギー効率が非常に高いですが、歩行の安定性が斜面の傾きに大きく影響されます。一般的に、各歩行機は特定の傾斜角に適した設計になっており、傾斜角が少し変わるだけでバランスを崩し、前方に倒れたり(傾斜角が大きすぎる場合)、歩行が止まったり(傾斜角が小さすぎる場合)することがあります。過去の研究では、足裏の曲率半径と斜面の傾斜角の関係が歩行の安定性に影響することが分かっています。
足裏形状の最適化
この問題を解決するため、足裏の形状を最適化し、単一のデザインで幅広い傾斜角に対応できる受動歩行機の設計を目指します。
評価関数
足裏形状を最適化するために、物理シミュレーション(OpenHRP3)と遺伝的アルゴリズムを組み合わせて、最適な形状を見つけました。
評価関数の設計は以下のフローチャートに示しています。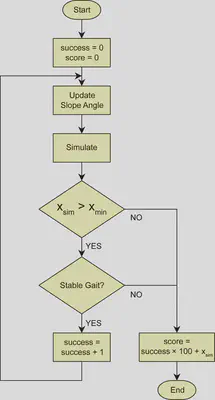
足裏形状の表現
足裏の形状は、9つの制御点をもつベジェ曲線で表現しました。足裏の内側と外側を合わせ、合計18の変数を遺伝子として扱いました。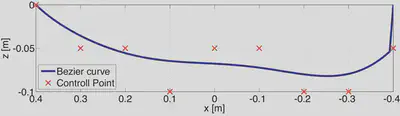
歩行の安定性分析
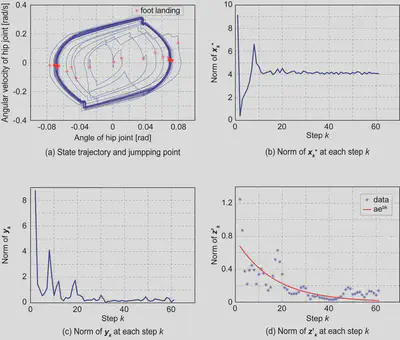
歩行の安定性を評価するために、リミットサイクル解析を用いました。リミットサイクルの安定性を確認するため、以下の手順でポアンカレ写像を使った解析を行いました。
- $k$ 歩目の着地を検出し、そのときの股関節角 $q_k^+$ と股関節角速度 $\dot{q}_k^+$ を使ってベクトル $\boldsymbol{x_k^+}$ を定義。 $$ \boldsymbol{x_k^+} = \begin{bmatrix} q_k^+ \\ \dot{q}_k^+ \end{bmatrix} $$
- $k-1$ 歩目の着地との差分を計算。 $$ \boldsymbol{y_k} = \boldsymbol{x_k^+} - \boldsymbol{x_{k-1}^+} $$
- 歩幅を使って正規化。 $$ \boldsymbol{z_k} = \boldsymbol{y_k} \oslash \frac{\boldsymbol{x_k^+} + \boldsymbol{x_{k-1}^+}}{2} $$
- 後方3点の移動平均を取り平滑化 $\boldsymbol{z’_k}$ したあと、指数関数でカーブフィッティング。 $$ ae^{bk} \approx |\boldsymbol{z'_k}| $$
- $b < 0$ なら、そのリミットサイクルは安定。
結果
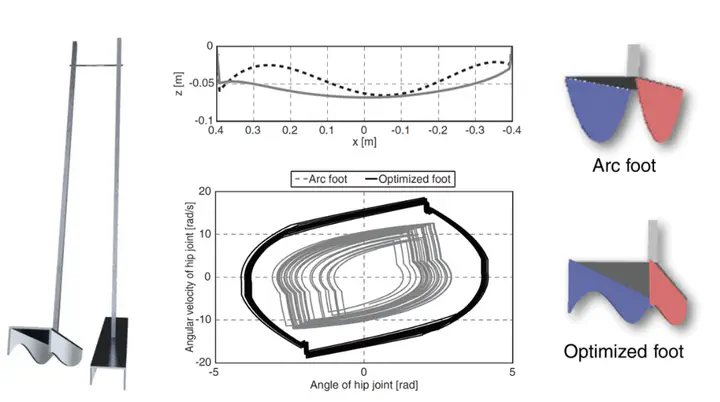
最適化した足裏形状を使うことで、従来の円弧型足裏形状と比べて、安定歩行が可能な傾斜角の範囲が 70% 拡大しました($2^\circ$ 〜 $7^\circ$)。さらに、リミットサイクルにおける着地状態のばらつきが 87% 減少しました。これにより、歩行の安定性が大幅に向上したことが示されました。


自己安定化の仕組み
最適化の結果、足裏の内側の曲率半径は $\frac{3}{4}l$、外側の曲率半径は $\frac{1}{4}l$ となりました($l$ は足裏の長さ)。
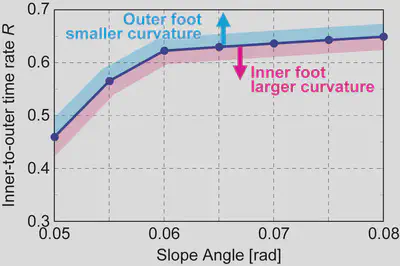
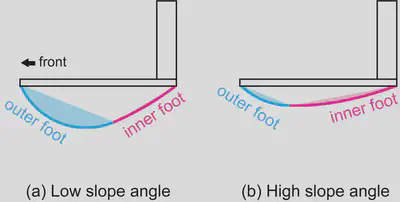
歩行中、歩行機のスイング運動により、まず内側の足裏が接地し、その後外側の足裏が接地する仕組みになっています。内側の足裏形状の接地時間と外側の足裏形状の接地時間の比($R$)を比較すると以下のようになりました。
- 傾斜が小さい場合 → 曲率半径の小さい外側が長く接地。
- 傾斜が大きい場合 → 曲率半径の大きい内側が長く接地。
この結果は、足裏形状と傾斜角の関係についての先行研究とも一致しており、最適化された足裏形状には自己安定化の仕組みが内在していることが示唆されました。