🚶 Passive Dynamic Walker

Last updated on Mar 1, 2025 Project

Optimizing Foot Shape of a Passive Dynamic Walker Enables Robust Walking Against Changes in Slope Inclination.

Table of Contents

Features

🦿 Passive Dynamic Walking: Walking utilizing gravity without actuators or controllers.
🚶 Morphological Intelligence: Utilizing body dynamics to generate energy-efficient walking, similar to biological organisms.
🦶 Optimized Foot Shape: Improved design enables stable walking even with changing slope inclinations.

Overview

Passive dynamic walkers achieve highly energy-efficient walking. However, a major challenge is that walking stability is easily disrupted when the slope inclination changes, posing a barrier to real-world implementation.
Previous research has improved stability by using different foot shapes tailored to specific inclinations. However, this approach requires a unique foot shape for each slope.
To address this, we propose a design method for a passive dynamic walker that can adapt to a wide range of slope inclinations using a single optimized foot shape.

What is Passive Dynamic Walking?

A passive dynamic walker utilizes gravity and its own dynamics to walk downhill. While this method is highly energy-efficient, walking stability is significantly influenced by the slope inclination.
Typically, each walker is designed for a specific inclination, meaning even a slight change in the slope can cause it to lose balance—either falling forward when the inclination is too steep or stopping when it is too shallow.
Previous studies have shown that the relationship between the curvature radius of the foot and the slope inclination affects walking stability.

Optimization of Foot Shape

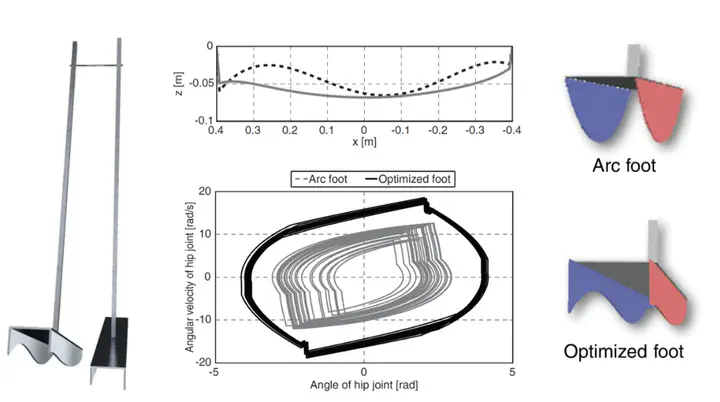
To address this issue, we optimized the foot shape, aiming to design a passive dynamic walker that can adapt to a wide range of slope inclinations with a single design.

Evaluation Function

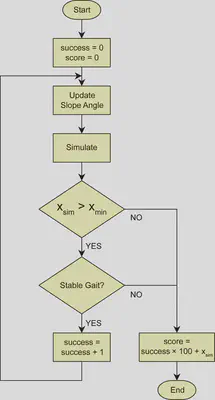
To optimize the foot shape, we used a combination of physical simulation (OpenHRP3) and a genetic algorithm to determine the optimal shape.
The design of the evaluation function is illustrated in the following flowchart.

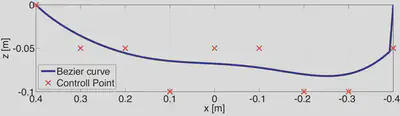
Representation of Foot Shape

The foot shape was represented using a Bézier curve with nine control points. Combining both the inner and outer sides of the foot, an numeric array with a total of 18 variables were treated as genes in the optimization process.

Gait Stability Analysis

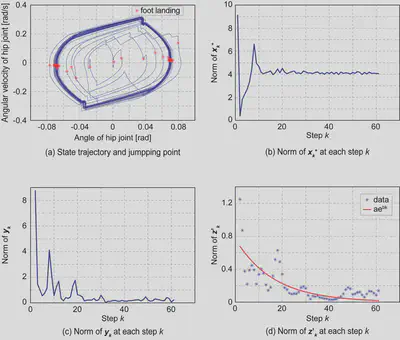
To evaluate gait stability, limit cycle analysis was used. To evaluate the stability of the limit cycle, an analysis using Poincaré map was conducted following these steps:

Detect the landing of the $k$-th step and define the vector $\boldsymbol{x_k^+}$ using the hip joint angle $q_k^+$ and the hip joint angular velocity $\dot{q}_k^+$ at that moment.
$$ \boldsymbol{x_k^+} = \begin{bmatrix} q_k^+ \\ \dot{q}_k^+ \end{bmatrix} $$
Compute the difference from the landing of the $(k-1)$-th step.
$$ \boldsymbol{y_k} = \boldsymbol{x_k^+} - \boldsymbol{x_{k-1}^+} $$
Normalize it using the step length.
$$ \boldsymbol{z_k} = \boldsymbol{y_k} \oslash \frac{\boldsymbol{x_k^+} + \boldsymbol{x_{k-1}^+}}{2} $$
Apply a moving average smoothing over the previous three points to obtain $\boldsymbol{z’_k}$, then perform curve fitting using an exponential function.
$$ ae^{bk} \approx |\boldsymbol{z'_k}| $$
If $b < 0$, the limit cycle is considered stable.

Results

By using the optimized foot shape, the range of inclination angles where stable walking is possible expanded by 70% compared to the conventional arc-shaped foot (from $2^\circ$ to $7^\circ$). Furthermore, the deviation in landing conditions within the limit cycle decreased by 87%. These results demonstrate a significant improvement in walking stability.

The passive dynamic walker with optimized feet

Comparison between the optimized foot and arc foot

Mechanism of Self-Stabilization

As a result of optimization, the curvature radius of the inner side of the foot was $\frac{3}{4}l$, while the curvature radius of the outer side was $\frac{1}{4}l$ ($l$ represents the length of the foot).

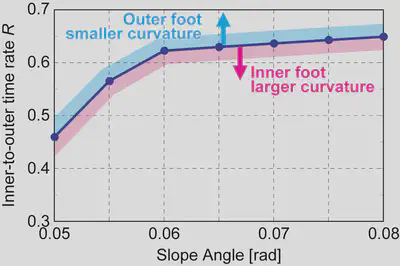
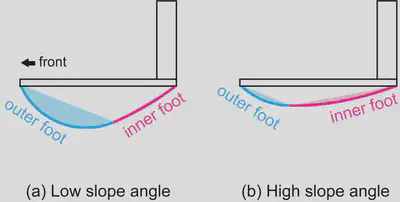
During walking, due to the swing motion of the walker, the inner side of the foot contacts the ground first, followed by the outer side. When comparing the ratio ($R$) of the contact time between the inner and outer foot shapes, the results were as follows:

For small slope inclination → The outer side, which has a smaller curvature radius, remains in contact longer.
For large slope inclination → The inner side, which has a larger curvature radius, remains in contact longer.

These results align with previous studies on the relationship between foot radius and inclination angle, suggesting that the optimized foot shape inherently possesses a self-stabilization mechanism.